Gamma是期权世界中的第五个希腊字母。在数学上,相对于其他四个希腊字母(Delta, Vega, Theta, Rho)不同,他实际是基于股票价格的二阶导数。在本视频中,我们将讲解最为重要的Gamma特性,理解为什么我们很难持有一张期权合约至到期日。
内容列表
希腊字母不是期权定价的结果,而是我们借用期权定价模型(如: Black-Scholes)分析期权的角度。
第一纬希腊字母
- 股票价格与执行价之间的关系产生了Delta:股票价格每波动$1,期权价格的变动幅度。
- 当前时点距离到期日的距离产生了Theta: 时间每过去1天,期权价格的变动幅度。
- 目前该股票的隐含波动率产生了Vega: 隐含波动率每波动1%,期权价格的变动幅度。
- 当前市场的无风险收益率产生了Rho: 无风险收益率Rf每波动1%,期权价格的变动幅度。
第二纬希腊字母
Gamma是Delta针对股票价格的再次求导,所以,Gamma是期权价格相对于股票价格的二阶导数。
Gamma定义
Delta = 30, Gamma = 5, 说明股票如果上升$1,期权价格将会增加$0.3,此后新的Delta将变成0.35(0.3+0.05)。未来股价再上升$1,期权价格就会增加$0.35。我们看到一个加速上升的现象。
线性市场与非线性市场的本质区别就是Gamma在线性市场中恒等于零,而在非线性市场中不为零。
Gamma曲线的特点
买入看涨期权 (Long Call) / 卖出看涨期权 (Short Call)
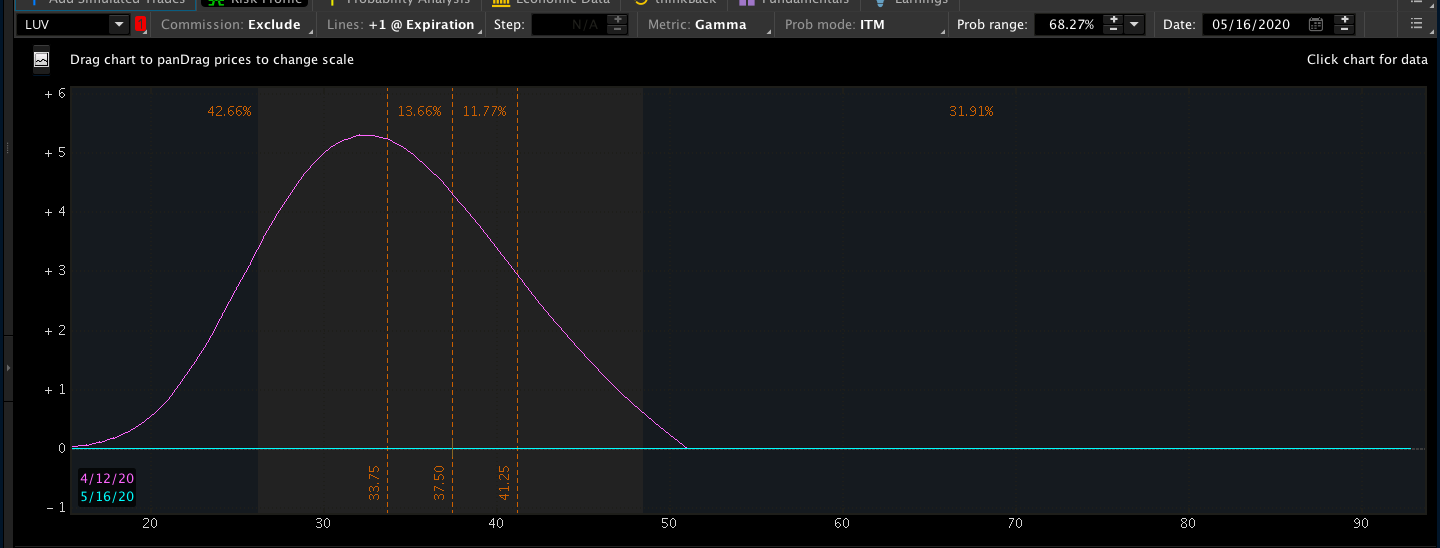
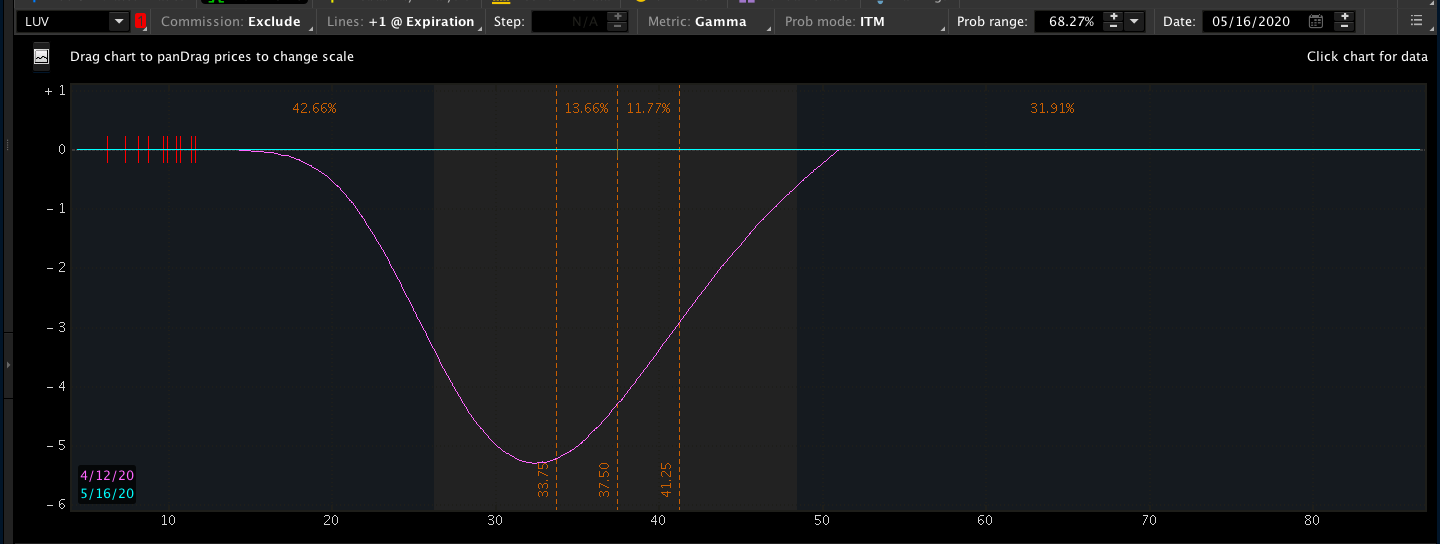
ATM附近的Gamma值最大 – 期权价格相对股票价格变动最为敏感。
随着到期日临近,
- Gamma曲线中间部分(平值附近*Around ATM)会逐渐抬高,而两边部分(OTM, ITM)会逐渐坍塌下去
- 处在平值附近的期权,会呈现相对原来距离到期日还比较远的时更大的波动速度。而OTM和ITM处的期权,将变动越来越不敏感。
Gamma的正负号
- 买入期权都是+Gamma
- 卖出期权都是-Gamma
规避Gamma风险
Gamma风险出现在临近到期日的平值附近(Around ATM)的期权合约,因此我们建议最简单的处理方法是提前拿掉期权头寸,彻底规避Gamma风险。
