谈一种被动且有效的投资体系,以及关于商品ETF提问的补充内容
本期内容分为上下两个部分。上半部用来回答投资者给SAM的邮件提问。由于最近$USO的事情,SAM收到了很多有关于这方面的问题,所以我整理了一下,选出代表性的一起讲解。下半部分,我将介绍一个好用又十分简单的偏被动型的投资小策略。这块内容的灵感也是来自与投资者的沟通。
本期内容分为上下两个部分。上半部用来回答投资者给SAM的邮件提问。由于最近$USO的事情,SAM收到了很多有关于这方面的问题,所以我整理了一下,选出代表性的一起讲解。下半部分,我将介绍一个好用又十分简单的偏被动型的投资小策略。这块内容的灵感也是来自与投资者的沟通。
$USO原油ETF基金2020年4月29日将进行1:8反向并股(Reverse Split).投资者持有股票或者期权头寸,应该如何应对,我在本影片做出了解答。
COVID-19来袭,金融市场大跌,我收到很多投资者咨询关于股票缩水的问题。首先,要明白任何人都有方向偏好(Directional Bias)。股票市场,大多数人都是多头。市场下跌,资产缩水是十分正常的事情。对冲,只能在一定程度起作用。然而,不应该发生的是资产大幅缩水,这是投资体系的问题。当出现这个问题如何处理,我介绍了如何巧妙使用期权策略进行完美撤退。同时也分析了策略的执行细节,和优缺点,从全方位理解这个策略。
Gamma是期权世界中的第五个希腊字母。在数学上,相对于其他四个希腊字母(Delta, Vega, Theta, Rho)不同,他实际是基于股票价格的二阶导数。在本视频中,我们将讲解最为重要的Gamma特性,理解为什么我们很难持有一张期权合约至到期日。
希腊字母不是期权定价的结果,而是我们借用期权定价模型(如: Black-Scholes)分析期权的角度。
Gamma是Delta针对股票价格的再次求导,所以,Gamma是期权价格相对于股票价格的二阶导数。
Delta = 30, Gamma = 5, 说明股票如果上升$1,期权价格将会增加$0.3,此后新的Delta将变成0.35(0.3+0.05)。未来股价再上升$1,期权价格就会增加$0.35。我们看到一个加速上升的现象。
线性市场与非线性市场的本质区别就是Gamma在线性市场中恒等于零,而在非线性市场中不为零。
买入看涨期权 (Long Call) / 卖出看涨期权 (Short Call)
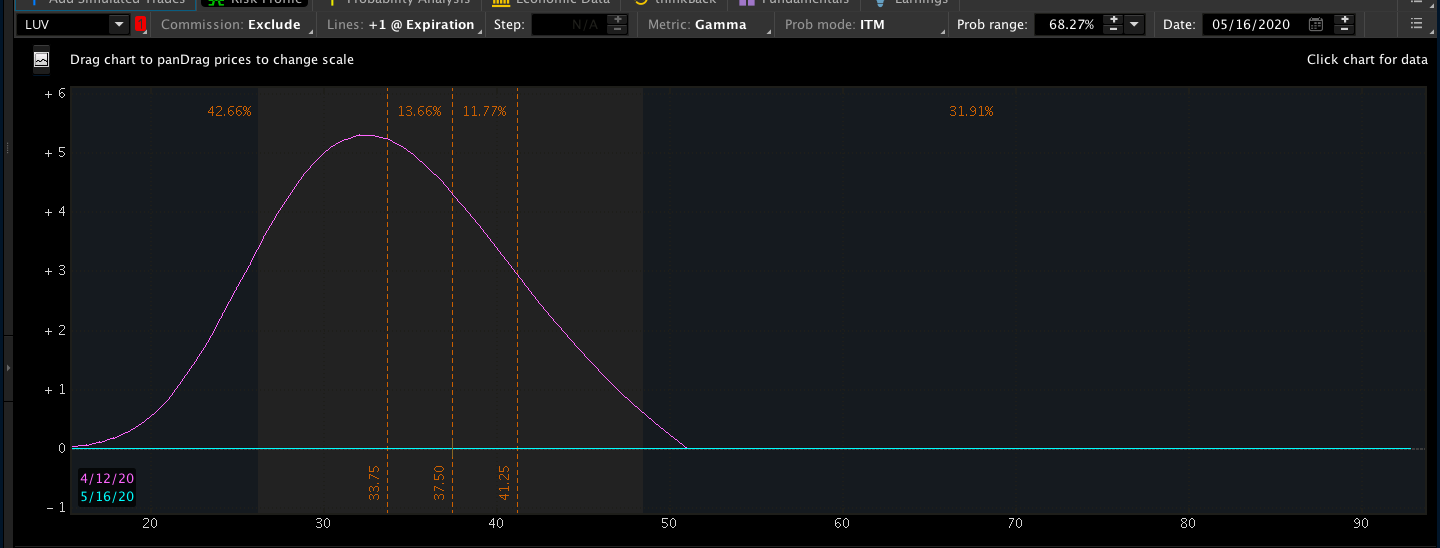
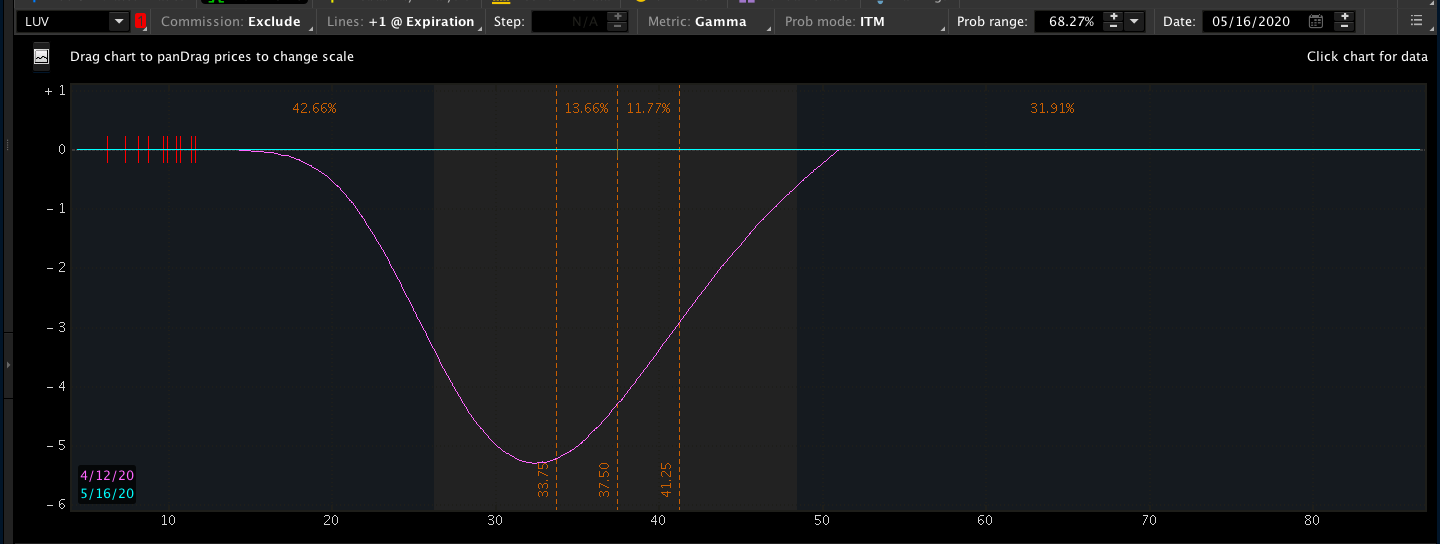
ATM附近的Gamma值最大 – 期权价格相对股票价格变动最为敏感。
随着到期日临近,
Gamma风险出现在临近到期日的平值附近(Around ATM)的期权合约,因此我们建议最简单的处理方法是提前拿掉期权头寸,彻底规避Gamma风险。
本集内容我介绍了美股市场的商品和能源ETF。这两种ETF追踪不同的市场,但结构类似。与其他市场ETF相比,他们有着不同的产品特性,会对你的投资产生显著影响。我用$USO为例,解释了这款ETF的利润构成,投资者应该在投资前做到心中有数,才能将它发挥最大的作用。
美股市场ETF品种众多,并以被动跟踪为主要构成。ETF的主要分类有以下几种:
今天我们讲的商品以及能源ETF属于非常特殊的一类金融工具。
我们以$USO(得克萨斯清甜原油ETF)为例,但是涉及的问题可以适用于绝大部份商品 / 能源ETF。
原油有现货市场,即$USOIL,其价格代表目前交割的原油的实际价格。$USO作为ETF,其价格的根本变动源自于现货市场价格的波动。当然,ETF作为资产包,通过金融工具的搭建还可能会包含其他引起价格变动的因素(下面详述)。
$USO使用了原油期货(/CL)进行跟踪原油的走势。由于/CL合约会到期,为了保持ETF的持续跟踪效果,$USO必须持续在每月合约到期前卖出手中老合约,同时买入下一个的新合约。
通过观察原油期限结构图(/CL Term Structure),我们发现随着到期日的推移,距离现在越远的合约价格不断升高。这种现象就是远期升水现象。形成原因主要是因为仓储成本、无风险收益率随时间增加而增大。
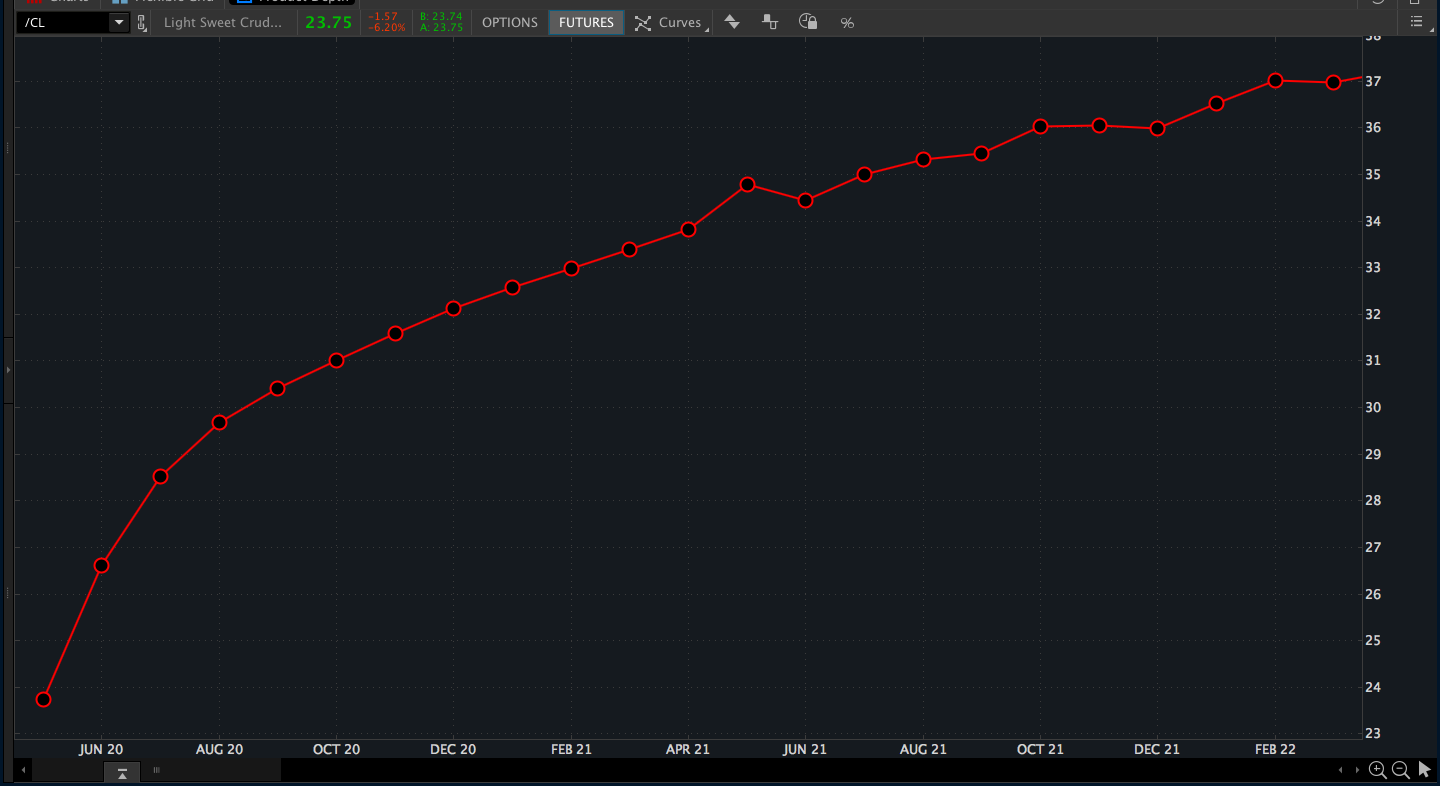
在存在远期升水的情况下,$USO卖出(低价)旧合约,买入(高价)新合约,造成亏损。亏损会被记入$USO的净值,最终反应$USO价格上。所以即使现货市场原油价格不变,由于期货合约调仓,$USO价格会被拉低。
原油市场的远期升水属于正常现象,但并不意味着市场常年存在远期升水 ——上个世界八十年代,原油市场就存在过多年的远期贴水(Backwardation)—— 期限结构图显示随着时间推移,价格反而下降。
由于现货原油需要巨大的仓储成本,ETF无法承受,使用原油期货合约跟踪是目前唯一可行的办法。
以期货为底的ETF存在以下调仓方法,并会在ETF的产品说明中披露。
不存在最好的调仓方法,只有适应目前市场环境的调仓方法。就目前市场环境来说,$USO并不适合长期(1周以上)持有。
由于期货合约存在金融杠杆,ETF只需要使用其中一部分资金购买期货合约,而剩下的资金可以用来投资到货币市场赚取无风险收益——该收益将抬高ETF的净值。在目前的低利率的市场环境下,这部分构成$USO价格的部分可以忽略。
Vega,期权第三个希腊字母(当然他不是真正的字母)衡量隐含波动率与期权价格的关系。本视频我分析了Vega在不同执行价的分布状况,以及为什么说Vega是一个很有威力的字母。